数学运算之最值问题知识框架

　数学运算问题一共分为十四个模块，其中一块是计算问题。最值问题是计算问题中算式计算里面的一种。

　　在近几年的公务员考试中，最值问题主要考查的是最大值和最小值，通常只有不等式法、求导法、二次函数法三种方法，其中以不等式法为主。只要掌握其规律及其解题技巧，便能轻松搞定该类问题（不等式法和求导法重点掌握）。

核心点拨

　　1、题型简介

　　最值问题一般为题目中出现“至多”、“至少”、“最多”、“最少”、“最大”、“最小”、“最快”、“最慢”、“最高”、“最低”等字样，通常采用不等式法、求导法等求最大值，最小值。

　　2、核心知识

　　（1）不等式法

　　正数的算术平均值不小于它们的几何平均数，即：

　　，当且仅当时，等号成立；

　　a2 +b2 ≥2ab，当且仅当a=b时，等号成立；

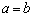　　（，当且仅当时，等号成立）；

　　（，当且仅当时，等号成立）。

　　（2）求导法

　　对于未知数的指数在二次以上的函数

　　经常使用求导法求最值：

　　当时，

　　求得的x值代人原式可以得到y的最值。

　　常见的是对二次方函数和三次方函数求导求最值，即

　　，

　　（3）二次函数法（了解）

　　二次函数：

　　当时，为最小值；

　　当时，为最大值。